受试者工作特征曲线（receiver operating characteristic curve，简称ROC曲线），是比较两个分类模型好坏的可视化工具   

ROC曲线的作用：

    1.较容易地查出任意界限值时的对类别的识别能力

    2.选择最佳的诊断界限值。ROC曲线越靠近左上角,试验的准确性就越高。最靠近左上角的ROC曲线的点是错误最少的最好阈值，其假阳性和假阴性的总数最少。

    3.两种或两种以上不同诊断试验对算法性能的比较。在对同一种算法的两种或两种以上诊断方法进行比较时，可将各试验的ROC曲线绘制到同一坐标中，以直观地鉴别优劣，靠近左上角的ROC曲线所代表的受试者工作最准确。亦可通过分别计算各个试验的ROC曲线下的面积(AUC)进行比较，哪一种试验的AUC最大，则哪一种试验的诊断价值最佳。

集才华与美丽于一身的ROC曲线到底是什么？

    ROC曲线是根据一系列不同的二分类方式（分界值或决定阈），以真阳性率TPR（灵敏度）为纵坐标，假阳性率FPR（1-特异度）为横坐标绘制的曲线。

那么TPR和FPR都是什么意思？先看下混淆矩阵

这样可以一目了然的看出正确分类和错误分类的样本数量，所以

准确率precision=（TP+TN）/（P+N）

    但是在实际应用中，我们感兴趣的类往往只占少数，所以在test集存在类不平衡的情况下，准确率对于我们的模型意义很小，eg：test中续费90，流失10，即使你把所有的样本预测为续费，准确率依然为90%，但对于我们感兴趣的流失用户而言，这个模型没有什么意义

所以，现实中我们更在乎的其实是召回率，即灵敏度，当然我们一般关注较高的是我们感兴趣类的召回率

recall =TP/（TP+FN）=TP/P

F度量则对准确率和召回率做一个权衡

F=（1+a2）*precision*recall/（a*precision+recall）

a2是a的平方，一般默认a= 1

说了这么多看似跟ROC没有相关的概念，但其实理解了上面的公式才能更好的理解ROC的作用，这里是美丽的分割线，下面是优美的ROC曲线

定义：

TPR = TP/P  即召回率公式

FPR = FP/N  即1-specificity

ROC曲线是以FPR为横坐标，以TPR为纵坐标，以概率为阈值来度量模型正确识别正实例的比例与模型错误的把负实例识别成正实例的比例之间的权衡，TPR的增加必定以FPR的增加为代价，ROC曲线下方的面积是模型准确率的度量

所以根据ROC曲线定义可知，绘制ROC要求模型必须能返回监测元组的类预测概率，根据概率对元组排序和定秩，并使正概率较大的在顶部，负概率较大的在底部进行画图

ROC曲线

    随机猜测的曲线是默认正负都按照0.5概率平均分类时的ROC曲线，那么离随机猜测曲线较远的点就是最好的概率选择阈值，该图中的凸包旁边点对应的概率就是我们所要选择的概率，即根据ROC凸点选择概率阈值和根据凸点判断两个模型好坏的由来。

 

 在分类模型中，ROC曲线和AUC值经常作为衡量一个模型拟合程度的指标

      sklearn上有一个画ROC曲线的例子，利用的是经典的鸢尾花（iris）数据。但鸢尾花数据分类的结果有三种，例子就直接来做图（一般的分类任务明明只有两种结果啊！！！），对于初学者来说（说的是我自己）看起来真的别扭。因此我对该例子做了一些改动（简化），将数据转化为二分类，这样比较容易理解。

       首先为大家介绍一下Python做ROC曲线的原理。sklearn.metrics有roc_curve, auc两个函数，ROC曲线上的点主要就是通过这两个函数计算出来的。

(1.)

    fpr, tpr, thresholds  =  roc_curve(y_test, scores) 

      其中y_test为测试集的结果，scores为模型预测的测试集得分（注意：通过decision_function(x_test)计算scores的值）；fpr,tpr,thresholds 分别为假正率、真正率和阈值。（应该是不同阈值下的真正率和假正率）。

(2.)

    roc_auc =auc(fpr, tpr) 

    roc_auc为计算的acu的值。

自己编写代码如下：

# -*- coding: utf-8 -*-import matplotlib.pyplot as pltfrom sklearn import svmfrom sklearn.metrics import roc_curve, auc  ###计算roc和auctrain_x = [[0.], [1.], [1.], [0.], [1.]]train_y = [0., 1., 1., 0., 1.]test_x = [[1.], [1.], [0.], [1.], [0.]]test_y = [1., 1., 0., 1., 0.]# Learn to predict each class against the othersvm = svm.SVC(kernel='linear', probability=True)###通过decision_function()计算得到的y_score的值，用在roc_curve()函数中model = svm.fit(train_x, train_y)test_y_score = model.decision_function(test_x)prediction = model.predict(test_x)print(test_y_score)print(prediction)# Compute ROC curve and ROC area for each classfpr, tpr, threshold = roc_curve(test_y, test_y_score)  ###计算真正率和假正率roc_auc = auc(fpr, tpr)  ###计算auc的值lw = 2plt.figure(figsize=(8, 5))plt.plot(fpr, tpr, color='darkorange',         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc)  ###假正率为横坐标，真正率为纵坐标做曲线plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')plt.xlim([0.0, 1.0])plt.ylim([0.0, 1.05])plt.xlabel('False Positive Rate')plt.ylabel('True Positive Rate')plt.title('Receiver operating characteristic example')plt.legend(loc="lower right")plt.show()

 

展示如下：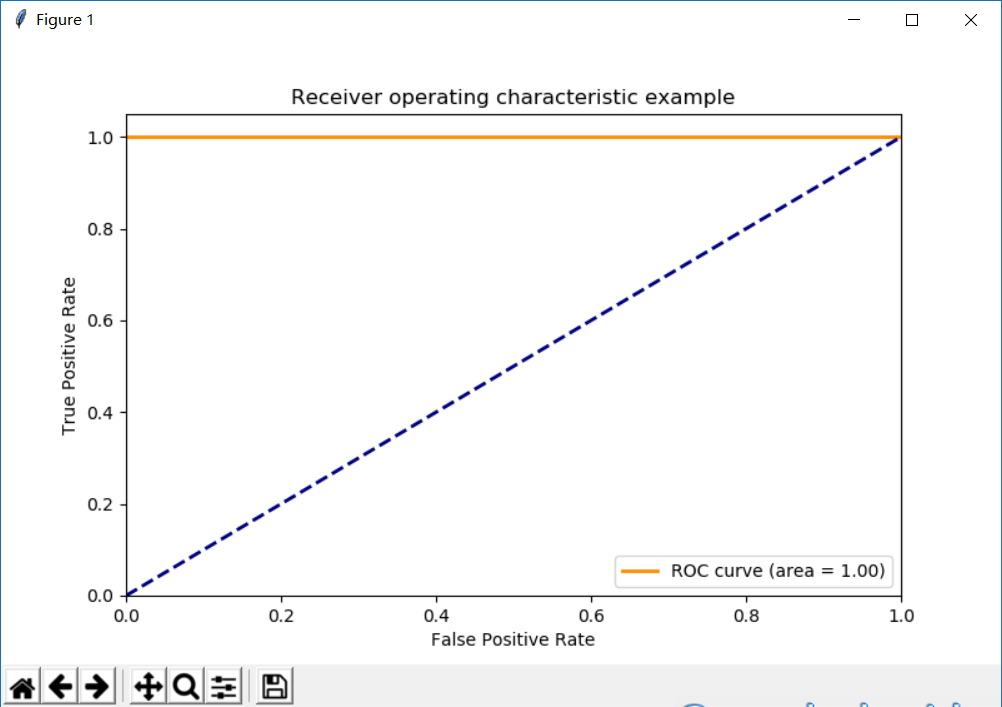

官网示例代码：

# -*- coding: utf-8 -*-"""Created on Thu Sep 21 16:13:04 2017@author: lizhen"""import numpy as npimport matplotlib.pyplot as pltfrom sklearn import svm, datasetsfrom sklearn.metrics import roc_curve, auc  ###计算roc和aucfrom sklearn import cross_validation # Import some data to play withiris = datasets.load_iris()X = iris.datay = iris.target ##变为2分类X, y = X[y != 2], y[y != 2] # Add noisy features to make the problem harderrandom_state = np.random.RandomState(0)n_samples, n_features = X.shapeX = np.c_[X, random_state.randn(n_samples, 200 * n_features)] # shuffle and split training and test setsX_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=.3,random_state=0) # Learn to predict each class against the othersvm = svm.SVC(kernel='linear', probability=True,random_state=random_state) ###通过decision_function()计算得到的y_score的值，用在roc_curve()函数中y_score = svm.fit(X_train, y_train).decision_function(X_test) # Compute ROC curve and ROC area for each classfpr,tpr,threshold = roc_curve(y_test, y_score) ###计算真正率和假正率roc_auc = auc(fpr,tpr) ###计算auc的值 plt.figure()lw = 2plt.figure(figsize=(10,10))plt.plot(fpr, tpr, color='darkorange',         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假正率为横坐标，真正率为纵坐标做曲线plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')plt.xlim([0.0, 1.0])plt.ylim([0.0, 1.05])plt.xlabel('False Positive Rate')plt.ylabel('True Positive Rate')plt.title('Receiver operating characteristic example')plt.legend(loc="lower right")plt.show()

 

参考博文：